Paddles and Collision

With a ball bouncing around the screen, we also want to give the user some way to control where the ball bounces. Enter: the paddle.

The block breaker paddle has an interesting feature, which is that when collisions with the paddle happen it behaves differently than a wall. The location at which the paddle is hit determines the direction the ball will move.

Spawning the Paddle

We’ll define the default size of a new paddle as well as how fast the paddle should be able to move as a const at the top of the file.

const DEFAULT_PADDLE_SIZE: Vec2 = Vec2::new(200.0, 20.0);
const PADDLE_SPEED: f32 = 400.0;

We’ll also define two new components. Paddle is a marker component so we can query for the paddle later, while HalfSize is useful for storing the size we need to construct the Aabb2d collider. The HalfSize component will store 1/2 of the width and height of the paddle.

#[derive(Component)]
struct Paddle;

#[derive(Debug, Component)]
struct HalfSize(Vec2);

In our startup function we can spawn the paddle with the default size and our new components. We position the paddle near the bottom of the screen, but the choice of exactly where to spawn it is fairly arbitrary.

commands.spawn((
    Sprite {
        custom_size: Some(DEFAULT_PADDLE_SIZE),
        color: SKY_50.into(),
        ..default()
    },
    Transform::from_xyz(
        0.0,
        -CANVAS_SIZE.y * (3. / 8.),
        0.0,
    ),
    Paddle,
    HalfSize(DEFAULT_PADDLE_SIZE / 2.),
));

Paddle Controls

We’ll let the player control the paddle next. Bevy provides a built-in resource to query keyboards, gamepads, and other input devices. In this case we want to use ButtonInput with KeyCode to react to keyboard input.

We’ll also query for our paddle’s Transform so that we can mutate it, filtered by the entities that have the Paddle component. Since we’re creating gameplay movement, we’ll also grab the Time resource again as well.

Then, for each paddle we queried, If the A or D keys are pressed, we move the paddle on the x axis using the PADDLE_SPEED and the delta time.

fn paddle_controls(
    input: Res<ButtonInput<KeyCode>>,
    mut paddles: Query<&mut Transform, With<Paddle>>,
    time: Res<Time>,
) {
    for mut transform in &mut paddles {
        if input.pressed(KeyCode::KeyA) {
            transform.translation.x -=
                PADDLE_SPEED * time.delta_secs();
        } else if input.pressed(KeyCode::KeyD) {
            transform.translation.x +=
                PADDLE_SPEED * time.delta_secs();
        }
    }
}

Also remember to add the paddle_controls system to the FixedUpdate schedule since it is gameplay related movement.

.add_systems(
    FixedUpdate,
    (paddle_controls, ball_movement),
)

Paddle Collision

It is time to implement paddle collision.

We’re going to do this in a generic way that will also work for bricks by taking advantage of the fact that the paddle and the bricks are both going to be the same kind of collider: an Aabb2d.

At the top of our ball_movement system, add two new queries. The first will be for all entities with a Transform and a HalfSize component, without the Ball component (because we’re using that one mutably in another query). We also get the Entity id which we’ll use to determine if the collider we’re working with is a paddle or a brick.

The second query is for all entities that have the Paddle component. We don’t need to query for any data here, so we use (). This is because Query::get accepts the Entity from the aabb_colliders query, and if that returns Some then we know the entity is a paddle!

fn ball_movement(
    mut balls: Query<
        (&mut Transform, &mut Velocity),
        With<Ball>,
    >,
    walls: Query<(&Wall, &Transform), Without<Ball>>,
    aabb_colliders: Query<
        (Entity, &Transform, &HalfSize),
        Without<Ball>,
    >,
    paddles: Query<(), With<Paddle>>,
    time: Res<Time>,
) {
    ...
}

In our ball_movement system we already have collision handling for walls, and ball movement handling. Our new Aabb2d collider code is going to go in between them.

for (wall, origin) in walls {
    ...
}

// Our new code goes here

transform.translation += (ball_movement_this_frame).extend(0.);

We will also be using a couple of new items here, so make sure to bring them into scope. These include constants for PI and 1/4 of PI, as well as FloatOrd, Aabb2d, and RayCast2d.

use std::f32::consts::{FRAC_PI_4, PI};

use bevy::{
    camera::ScalingMode,
    color::palettes::tailwind::*,
    math::{
        FloatOrd,
        bounding::{Aabb2d, RayCast2d},
    },
    prelude::*,
};

Now for the actual collision code.

RayCast2d takes the Ray2d we used in a previous lesson and limits it to a specific distance. It also includes RayCast2d::aabb_intersection_at which will tell us where our ray hit on an Aabb2d within that distance away.

Our ball only moves a set distance every frame, so this is very useful!

let ball_cast = RayCast2d::from_ray(
    ball_ray,
    ball_move_distance,
);

We then take our aabb_colliders query and iterate over it, constructing the Aabb2d from the position and half size of our collider. If our RayCast2d::aabb_intersection_at doesn’t hit the collider, then we know this collider isn’t in our path this frame and can filter it out using ?, which returns None to our filter_map.

Otherwise, we have a hit within the appropriate distance, so we return the data we want in a tuple alongside the distance away the hit occurs.

Using that distance, we can sort the results. We only want the closest hit, since to hit anything further away the ray would have to go through the closest hit first.

To sort by f32, we need to use one of Bevy’s helpers: FloatOrd. FloatOrd wraps an f32 and gives it an order that deviates from the spec by sorting NaN as the lowest possible number. That’s fine for us since we don’t plan to have NaN here.

aabb_colliders
    .iter()
    .filter_map(
        |(entity, origin, half_size)| {
            let aabb_collider = Aabb2d::new(
                origin.translation.xy(),
                half_size.0,
            );

            // no intersection means no hit distance
            let hit_distance = ball_cast
                .aabb_intersection_at(
                    &aabb_collider,
                )?;

            Some((
                entity,
                origin,
                aabb_collider,
                hit_distance,
            ))
        },
    )
    .min_by_key(|(_, _, _, distance)| {
        FloatOrd(*distance)
    })

We then wrap this in an if-let. If the Some pattern matches the result from our min_by_key, then we have the closest hit to work with. Otherwise we don’t have a hit and can skip the collision logic.

if let Some((entity, origin, _aabb_collider, _)) =
    aabb_colliders
        .iter()
        .filter_map(...)
        .min_by_key(...)
{
    // new code goes in here
}

Inside of our if-let, we know we have a hit and the first decision we make is if we hit a paddle or not. We do this like we talked about earlier, using Query::get and checking to see if the Result returned is_ok, which means the Entity we passed in is in the query set for paddles.

if paddles.get(entity).is_ok() {
    let direction_vector =
        transform.translation.xy()
            - origin.translation.xy();

    let angle = direction_vector.to_angle();
    let linear_angle = angle.clamp(0., PI) / PI;
    let softened_angle = FRAC_PI_4
        .lerp(PI - FRAC_PI_4, linear_angle);
    velocity.0 =
        Vec2::from_angle(softened_angle)
            * velocity.0.length()
} else {
    // handle bricks!
}
break;

Once we have a collision we have to do a bit of math, which we’ll walk through step by step.

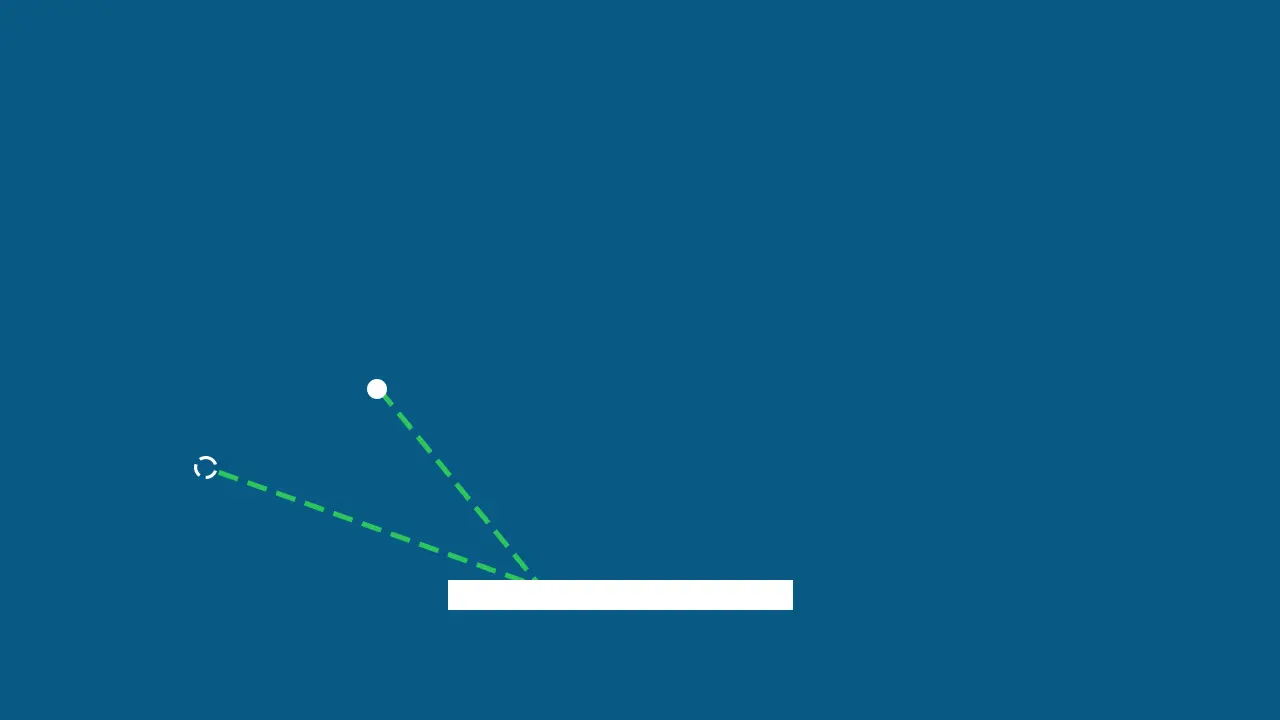
What we have is two points:

• the ball’s position
• the paddle’s position

We can get the vector between them by subtracting the two Vec2s. If you think of the Vec2 from 0,0 to each point (0,0 to ball and 0,0 to paddle), then subtracting those two vectors gives us the “third side of the triangle” which is the vector between the ball and the paddle.

We tend to measure angles in Radians instead of degrees when programming, so we can get the angle of our ball-to-paddle vector calling Vec2::to_angle.

This will give us the angle value in radians. A full circle in radians is 2 * PI, or approximately 6.28. We only want to deal with the top half of the circle here, so we’ll clamp the value from 0 to PI (which is basically 0-180 degrees).

This is a bit too extreme of an angle though, since we really never want to shoot the ball away from the paddle horizontally. To fix this, we’ll divide our 0-PI value by PI to get a 0-1 value. This 0-1 value can then be linearly interpolated (or “LERP”d) into a different range of values. For us, we’ll choose a 90 degree angle’s worth of values, from FRAC_PI_4 to PI - FRAC_PI_4. These angles are the 90 degrees directly up from the middle of the paddle on either x axis.

Once we have our “softened angle” to avoid horizontals, we can take the radians value and convert it back to a Vec2. This gives us the direction, but we still want the original speed we were going, so we multiply the direction by the velocity length to maintain our speed.

velocity.0 = Vec2::from_angle(softened_angle) * velocity.0.length()

This sends the ball off in the direction of the angle from the center of the paddle. An incoming ball from the right, that hits the right side of the paddle.

Will bounce back off to the right instead of the left like a regular reflection would.

At the very end of our collision logic, we need to add a break so that the regular ball movement isn’t applied. The full ball_movement system now looks like this.

fn ball_movement(
    mut balls: Query<
        (&mut Transform, &mut Velocity),
        With<Ball>,
    >,
    walls: Query<(&Wall, &Transform), Without<Ball>>,
    aabb_colliders: Query<
        (Entity, &Transform, &HalfSize),
        Without<Ball>,
    >,
    paddles: Query<(), With<Paddle>>,
    time: Res<Time>,
) {
    for (mut transform, mut velocity) in &mut balls {
        // a ray that casts infinitely in the direction
        // the ball is moving
        let ball_ray = Ray2d::new(
            // the location of the ball
            transform.translation.xy(),
            // the Direction the ball is moving in
            Dir2::new(velocity.0).unwrap(),
        );

        // how far the ball is going to go this frame
        // represented as a vec2
        let ball_movement_this_frame =
            velocity.0 * time.delta_secs();
        let ball_move_distance =
            ball_movement_this_frame.length();

        // for each wall, check if we're going to hit it this frame
        for (wall, origin) in walls {
            if let Some(hit_distance) = ball_ray
                .intersect_plane(
                    origin.translation.xy(),
                    wall.0,
                )
                && hit_distance <= ball_move_distance
            {
                // velocity is just the reflection of the hit
                // this is basically inverting the X or Y direction
                // to move in the opposite direction
                velocity.0 = velocity
                    .0
                    .reflect(wall.0.normal.as_vec2());
                return;
            }
        }

        let ball_cast = RayCast2d::from_ray(
            ball_ray,
            ball_move_distance,
        );

        // for each brick or paddle, check if we're going to hit it this frame.
        // then take the closest hit and process it, if it exists.
        if let Some((entity, origin, _aabb_collider, _)) =
            aabb_colliders
                .iter()
                .filter_map(
                    |(entity, origin, half_size)| {
                        let aabb_collider = Aabb2d::new(
                            origin.translation.xy(),
                            half_size.0,
                        );

                        // no intersection means no hit distance
                        let hit_distance = ball_cast
                            .aabb_intersection_at(
                                &aabb_collider,
                            )?;

                        Some((
                            entity,
                            origin,
                            aabb_collider,
                            hit_distance,
                        ))
                    },
                )
                .min_by_key(|(_, _, _, distance)| {
                    FloatOrd(*distance)
                })
        {
            if paddles.get(entity).is_ok() {
                let direction_vector =
                    transform.translation.xy()
                        - origin.translation.xy();

                let angle = direction_vector.to_angle();
                let linear_angle = angle.clamp(0., PI) / PI;
                let softened_angle = FRAC_PI_4
                    .lerp(PI - FRAC_PI_4, linear_angle);
                velocity.0 =
                    Vec2::from_angle(softened_angle)
                        * velocity.0.length()
            } else {
                // handle bricks!
            }
            break;
        }

        transform.translation +=
            (ball_movement_this_frame).extend(0.);
    }
}